Containment

The crate also allows for containment checks for every topological structure. They work by ray casting and checking the normal at the intersection with the boundary. This also works for edge cases when the casted ray hits a corner.

This works for various faces. Red means outside, green means inside, blue means on the edge, and gray means on the corner.

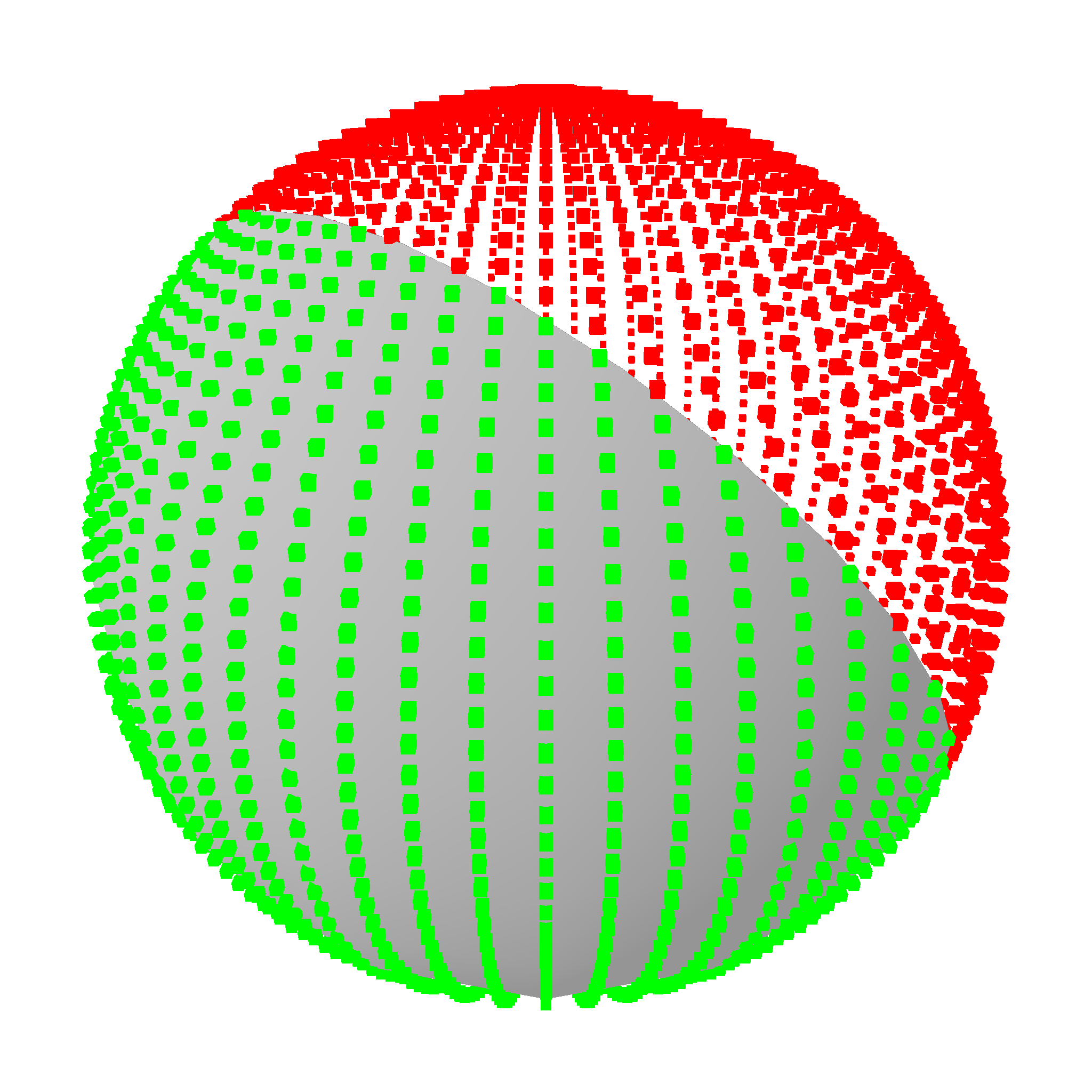
And also for various volumes.

TODO: Add images

Why cant we just count the intersections?

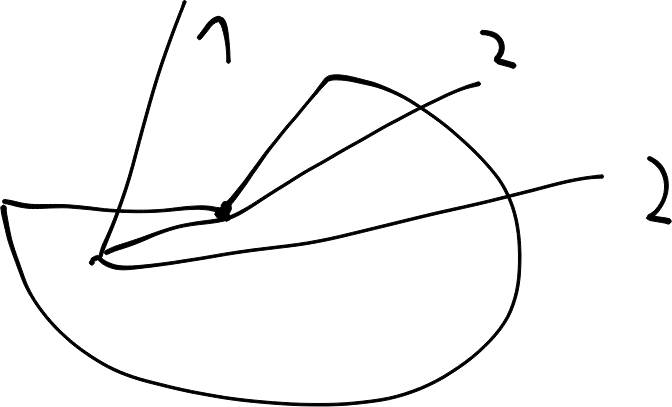
Imagine we are at a corner of a contour. We want to check if a point is inside or outside the contour. We can do this by drawing a line from the point to the corner (ray). If the line crosses the contour an odd number of times, the point is inside the contour. If the line crosses the contour an even number of times, the point is outside the contour.

However, this method is not perfect. If we pass through a corner, the method might miscount the number of intersections. So we have to make sure we do not pass through a corner.

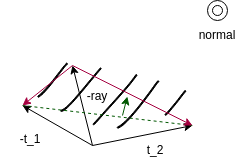
Alternatifly, we can also take a look at the direction of the closest intersection. If we normalize -ray, -tangent_1 and tangent_2, if -ray is on the top side of the green dashed line, we know it comes from inside. We can also create a coordinate system (red lines and normal) and check its handedness. It switches handed ness when -ray is crossing the contour. This is a more robust method, fully deterministic and deals with the edge case.

A common idea is also to check the normals. If the ray is \(n \cdot d\) is positive for both normals \(n\) and the direction of the ray \(d\), we know we are inside the contour. This is true. But depending on if it is a concave or convex corner, it is sufficient that one of the dot products is positive (area 2 and 4), or both have to be positive (area 1).

Three dimensional case

Same idea. If the coordinate system changes handedness, we know we are inside the corner.